深度学习从0到1——深度学习概论

深度学习从0到1——深度学习概论
王貔貅本文转载自百度AI飞浆
深度学习概论
人工智能&机器学习&深度学习
在研究深度学习之前,先从三个概念的正本清源开始。概括来说,人工智能、机器学习和深度学习覆盖的技术范畴是逐层递减的,三者的关系:人工智能 > 机器学习 > 深度学习。
人工智能是最早出现的,范围也最广;随后出现的是机器学习;最内层的是深度学习,也是当今人工智能大爆炸的核心驱动力。

简单来说,机器学习是实现人工智能的方法,深度学习是实现机器学习的技术之一。也可以说,机器学习是人工智能的子集,而深度学习是机器学习的子集。接下来我们分别看一看这三者具体包含了什么。
【人工智能】
人工智能(Artificial Intelligence, AI) 是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。
人工智能是计算机科学的一个分支,它企图了解智能的实质,并生产出一种新的能以人类智能相似的方式做出反应的智能机器,该领域的研究包括机器人、语言识别、图像识别、自然语言处理等。

2006 至今,大数据分析的需求,神经网络又被重视,成为深度学习理论的基础。
到目前为止,人工智能在人们日常生活中各个领域的普及度日趋升高。相对于初期发展阶段而言,人工智能的实用性、应用价值均产生了较为明显的变化。i am AI
【机器学习】
卡内基梅隆大学的Tom Michael Mitchell 教授在 1997 年出版的书籍《机器学习》中对机器学习(Machine Learning) 做了非常专业的定义:如果一个程序可以在任务T上,随着经验E的增加,效果P也可以随之增加,则称这个程序可以从经验中学习。以下棋为例,设计出的程序可以随着对弈盘数的增加而不断修正自己的下棋策略,使得获胜率不断提高,就认为这个程序可以在经验中学习。
机器学习是从人工智能中产生的一个重要学科分支,是实现智能化的关键。
但传统的机器学习在使用过程中存在着不可避免的问题。传统机器学习最关键的问题是必须依赖给定数据的表示,而实际上,在大多数任务中我们很难知道应该提取哪些特征。例如我们想要在一堆动物的图片中辨认出猫,试图通过胡须、耳朵、尾巴等元素的存在与否来辨认,但如果照片中存在很多遮挡物,或是猫的姿势发生了改变等,都会影响到机器识别。
找不到一个合理的方法提取数据,这就使得问题变得棘手。
深度学习采用深层网络结构,具备了强大的特征学习能力,从而解决了机器学习的核心问题。
【深度学习】
机器学习算法理论在上个世纪90年代发展成熟,在许多领域都取得了成功,但平静的日子只延续到2010年左右。随着大数据的涌现和计算机算力提升,深度学习模型异军突起,极大改变了机器学习的应用格局。今天,多数机器学习任务都可以使用深度学习模型解决,尤其在语音、计算机视觉和自然语言处理等领域,深度学习模型的效果比传统机器学习算法有显著提升。
2016年,AlphaGo 击败韩国围棋冠军李世石,在媒体报道中,曾多次提及“深度学习”这个概念。而新版本的AlphaGoZero,更充分地运用了深度学习法,不再从人类棋手的以往棋谱记录中开始训练,而是完全靠自己的学习算法,通过自我对弈来学会下棋。经过一段时间的自我学习,它就击败了曾打败李世石的以及曾完胜柯洁的AlphaGo版本。

深度学习作为目前机器学习领域最受关注的分支,是用于实现人工智能的关键技术,相比较于传统的机器学习,深度学习不再需要人工的方式提取特征,而是自动从简单特征中提取,组合更复杂的特征,从数据中学习到复杂的特征表达形式并使用这些组合特征解决问题。
通过以上描述可以简单理解为,深度学习是基于多层神经网络的、以海量数据为输入的规则自学习方法。深度学习可以获得更好的方法来表示数据的特征,同时由于模型的层次深、表达能力强,因此有能力处理大规模数据。对于图像、语音这种直接特征不明显的问题,深度模型能够在大规模训练数据上取得更好的效果。
早期的深度学习可以理解为传统神经网络的拓展,二者的相同之处在于,深度学习采用了与神经网络相似的分层结构:包括输入层、隐藏层、输出层的多层网络。关于神经网络,我们会在之后的章节展开论述。
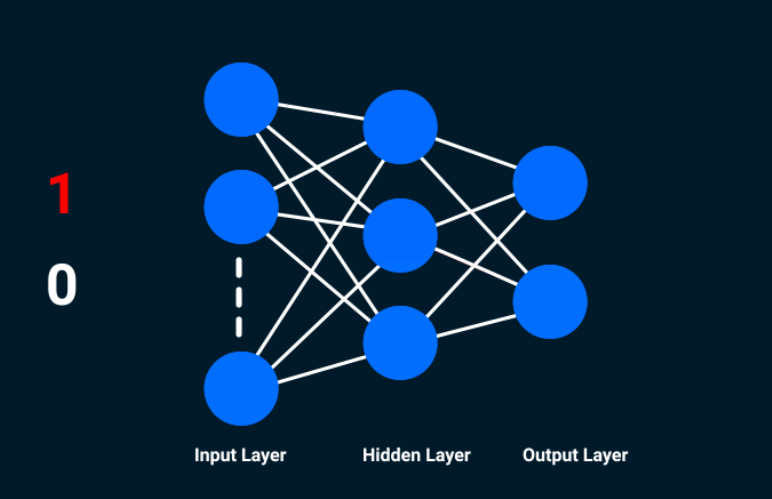
深度学习基本概念
深度学习崛起的时代背景
谈到深度学习的历史不得不追溯到神经网络技术。深度学习崛起之前,神经网络曾经历两次高潮与两次低谷。
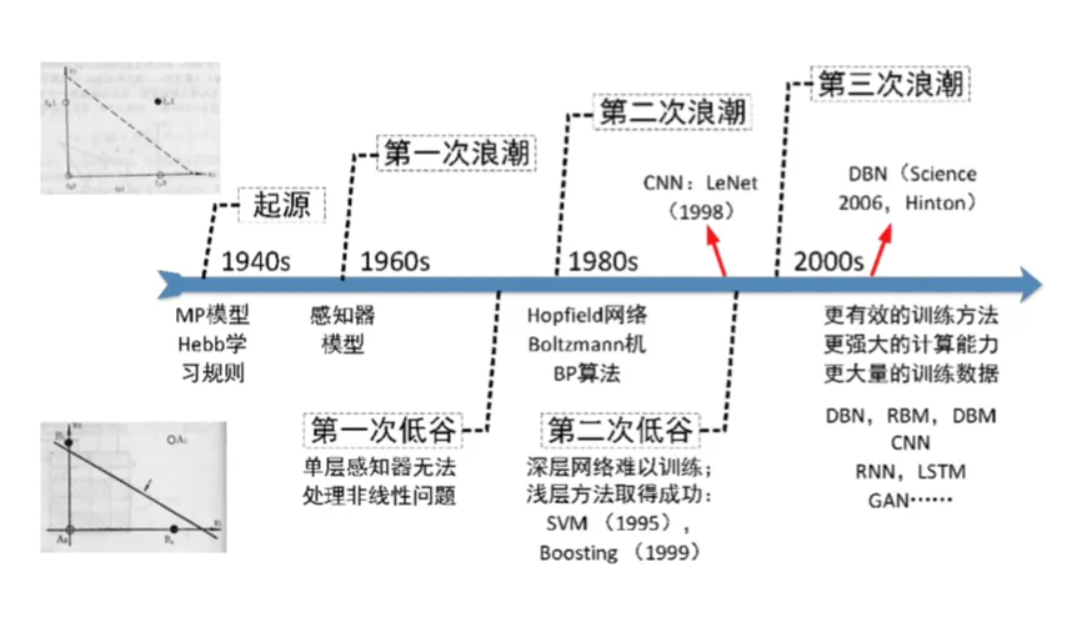
纵使神经网络又一次进入寒冬,但杰弗里·辛顿等人仍然没有放弃。2006年,辛顿在论文 A Fast Learning Algorithm for Deep Belief Nets 中介绍了一种成功训练多层神经网络的方法,他将这种神经网络成为深度信念网络。
辛顿提出了两个观点:①多层人工神经网络模型有很强的特征学习能力,深度学习模型得到的特征数据相对于原始数据有更本质的代表性,这将大大提高分类识别的能力;②对于深度神经网络很难通过训练达到最优的问题,可以采取逐层训练的方法解决,将上一层训练好的结果作为下层训练过程中的初始化参数。
由此,神经网络实现了最新的一次突破——深度学习。
深度学习的诞生伴随着更优化的算法、更高性能的计算能力(GPU)和更大的数据集的时代背景。使用GPU集群可以将原来一个月才能训练出的网络加速到几小时就能完成,除了硬件的飞速发展为其提供条件以外,深度学习还得到了充分的燃料:大数据。相较传统的神经网络,尽管在算法上我们确实简化了深度架构的训练,但最重要的进展还是我们有了成功训练这些算法的资源。可以说,人工智能只有在数据的驱动下才能实现深度学习,不断迭代模型,变得越来越智能。
因此,想要持续发展深度学习技术,算法、硬件和大数据缺一不可。
常见的深度学习网络结构
深度学习可以应用在各大领域中,根据应用的情况不同,深度神经网络的形态也各不相同。常见的深度学习模型主要有全连接神经网络(Fully Connected Netural Network,FCN) 、卷积神经网络(convolutional neural network, CNN) 和循环神经网络(Recurrent neural network,RNN) 。他们均有着自身的特点,并在不同的场景中发挥着重要的作用。
【全连接神经网络】
全连接神经网络是一种连接方式较为简单的人工神经网络结构,全连接层的每一个节点都与上一层的所有节点相连。多层感知机(Multi-Layer Perception,MLP) 就属于全连接网络,MLP 网络是可以应用于几乎所有任务的多功能学习方法,包括分类、回归,甚至是无监督学习。
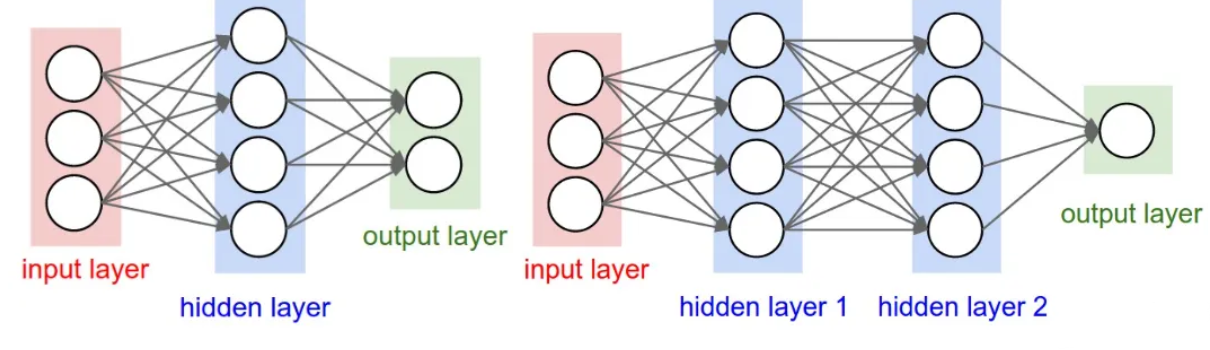
然而由于全连接层所有的输出和输入都是相连的,一般全连接层的参数是最多的,这需要相当数量的存储和计算空间。参数的冗杂问题使得单纯的FC组成的常规神经网络很少会被用于较为复杂的场景中。常规神经网络一般用于依赖所有特征的简单场景,比如我们接下来会介绍的房价预测模型使用的就是相对标准的全连接神经网络。
【卷积神经网络】
卷积神经网络是一种专门用来处理具有类似网络结构的数据的神经网络,如图像数据。与FC不同的地方在于,CNN的上下层神经元并不都能直接连接,而是通过卷积核(convolution kernel) 作为中介,通过核的共享,大大减少了隐藏层的参数。
简单的CNN是一系列层,并且每个层都通过一个可微函数将一个量转化为另一个量,这些层主要包括卷积层(Convolutional layer)、池化层(Pooling layer) 和全连接层(FC layer) 。
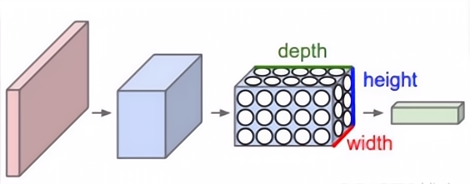
【循环神经网络】
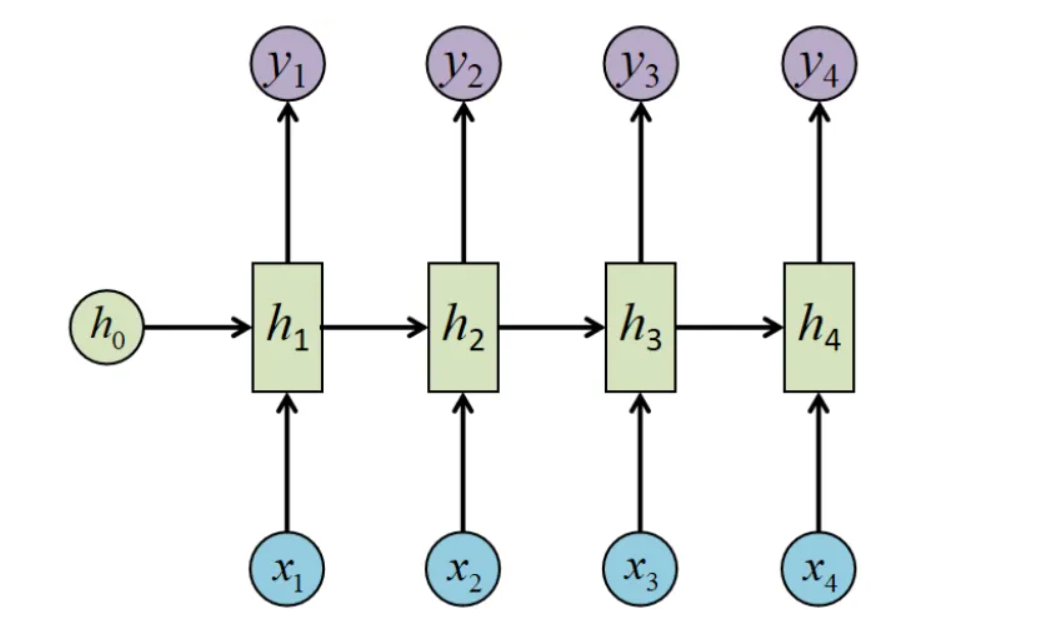
循环神经网络也是常用的深度学习模型之一,就像CNN是专门用于处理网格化数据的神经网络,RNN是一种用于处理序列数据的神经网络。如音频中含有时间成分,因此音频可以被表示为一维时间序列;语言中的单词都是逐个出现的,因此语言的表示方式也是序列数据。RNN在机器翻译、语音识别等领域中均有非常好的表现。
机器学习基础
在了解了深度学习的概念之后,本节将会以机器学习的相关概念作为切入点,来使用代码实现基本的神经网络模型,这些实验方法在深度学习中也同样使用。
机器学习一般过程
机器学习有三个主要的组成部分:经验Experience(E)、任务Task(T)、任务完成效果的衡量指标Performance measure(P)。有了这三个概念,机器学习的定义可以表述为:在有了经验E的帮助后,机器完成任务T的衡量指标P会变得更好。
本节从构造模型的角度将机器学习理解为:从数据中产生模型的过程。机器学习的过程如下:输入训练数据,利用特定的机器学习方法建立估计函数。在训练得到函数后,可将测试数据输入该函数,该函数的输出即预测结果。
机器学习的方法
(1)有监督学习(supervised learning)
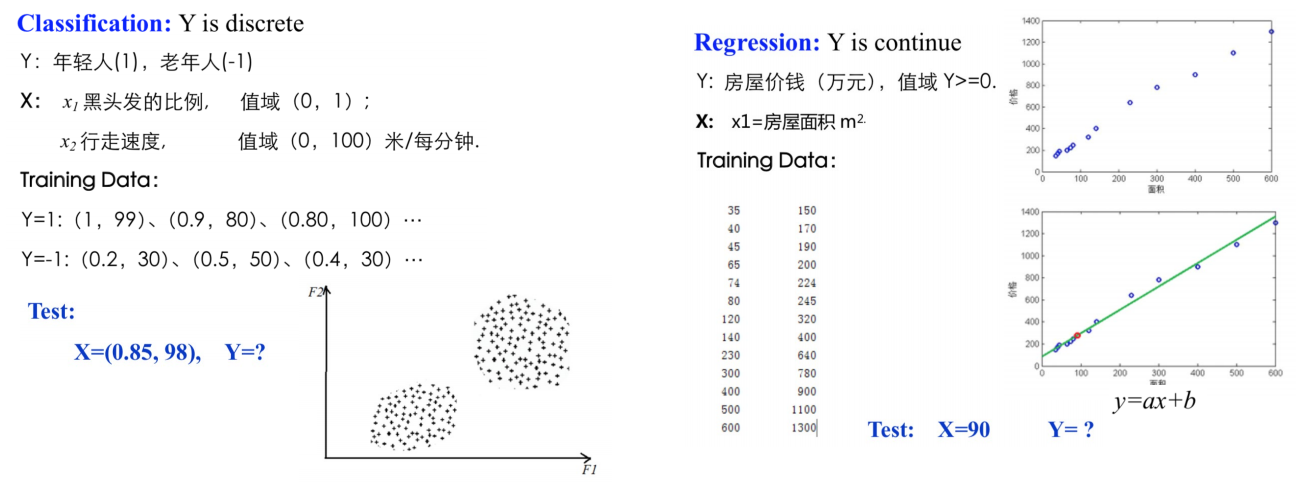
从给定的有标注的训练数据集中学习出一个函数(模型参数),当新的数据到来时可以根据这个函数预测结果。 常见任务包括分类与回归。
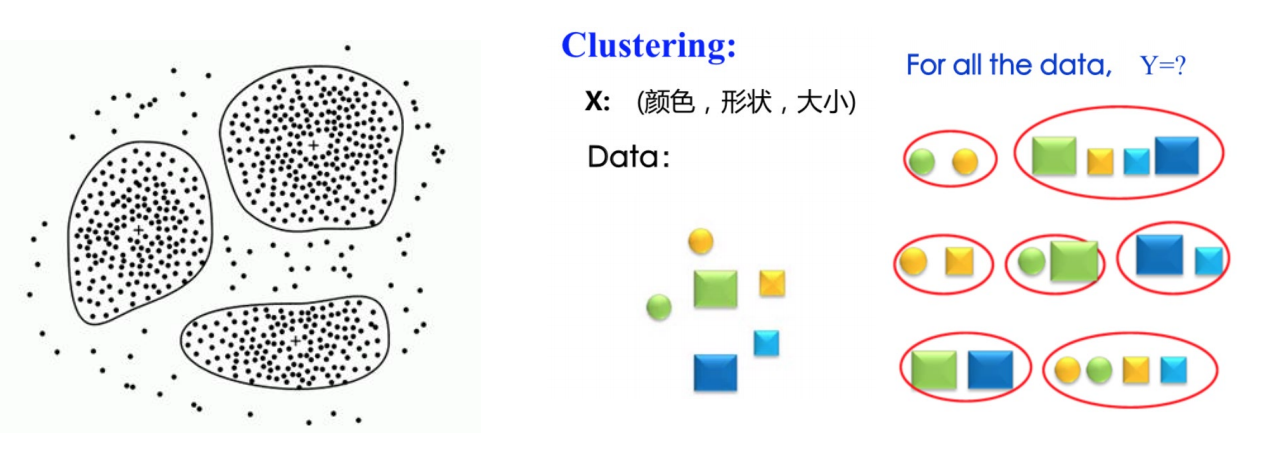
(2)无监督学习(unsupervised learning)
使用没有标注的训练数据集,需要根据样本间的统计规律对样本集进行分析,常见任务如聚类等。
(3)半监督学习(Semi-supervised learning)
结合(少量的)标注训练数据和(大量的)未标注数据来进行数据的分类学习。
(4)强化学习(Reinforcement Learning)
外部环境对输出只给出评价信息而非正确答案,学习机通过强化受奖励的动作来改善自身的性能。
如:让计算机学着去玩Flappy Bird

我们不需要设置具体的策略,比如先飞到上面,再飞到下面,我们只是需要给算法定一个“小目标”!比如当计算机玩的好的时候,我们就给它一定的奖励,它玩的不好的时候,就给它一定的惩罚,在这个算法框架下,它就可以越来越好,超过人类玩家的水平。
机器学习的准备
机器学习的实现可以分成两步:训练和预测,类似于归纳和演绎:
归纳: 从具体案例中抽象一般规律,机器学习中的“训练”亦是如此。从一定数量的样本(已知模型输入和模型输出)中,学习输出与输入的关系(可以想象成是某种表达式)。
演绎: 从一般规律推导出具体案例的结果,机器学习中的“预测”亦是如此。基于训练得到的与之间的关系,如出现新的输入,计算出输出。通常情况下,如果通过模型计算的输出和真实场景的输出一致,则说明模型是有效的。
【特征工程】


特征工程,是指用一系列工程化的方式从原始数据中筛选出更好的数据特征,以提升模型的训练效果。业内有一句广为流传的话是:数据和特征决定了机器学习的上限,而模型和算法是在逼近这个上限而已。由此可见,好的数据和特征是模型和算法发挥更大的作用的前提。
特征工程通常包括数据预处理、特征选择、降维等环节。
1.数据预处理
真实世界的数据通常包含噪声、缺失值,并且可能采用无法直接用于机器学习模型的不可用格式。当收集到真实数据后,往往不能直接使用,要根据数据的具体情况来进行针对性的处理。

- 数据清洗
对各种脏数据进行对应方式的处理,得到标准、干净、连续的数据,提供给数据统计、数据挖掘等使用。数据的完整性、数据的合法性、数据的唯一性、数据的权威性以及数据的一致性等。 - 数据采样
要避免数据的不平衡(数据集的类别分布不均)。 - 数据集拆分
训练数据集、验证数据集、测试数据集。-折交叉验证法:把训练样例分成份,然后进行次交叉验证过程,每次使用不同的一份样本作为验证集合,其余份样本合并作为训练集合。
2.特征选择
请看下面这张图片并思考,所有特征都有用吗?
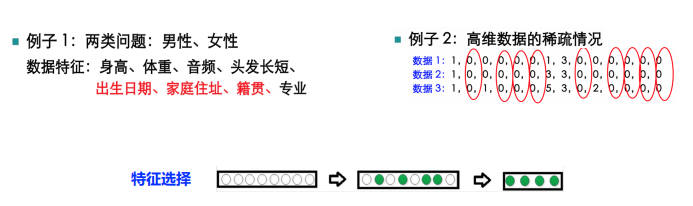
特征选择方法比较简单粗暴,直接将不重要的特征删除。特征选择方法主要包括三大类:过滤法(Filter)、包装法(Wrapper) 和嵌入法(Embedded)。
- 过滤法:根据发散性或者相关性对各个特征进行评分,通过设定阈值或者待选择阈值的个数来选择特征。
- 包装法:根据目标函数(通常是预测效果评分)每次选择若干特征,或者排除若干特征。包装法的思路是将最终要用的学习器的性能作为特征子集的评价准则。
- 嵌入法:是一种让算法自己决定使用哪些特征的方法,即特征选择和算法训练同时进行。在使用嵌入法时,我们先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据权值系数从大到小选择特征。
3.特征降维
特征选择完成后,可能由于特征矩阵过大,导致计算量大、训练时间长,因此降低特征矩阵维度也是必不可少的。特征降维主要是通过映射变换方法,将高维特征向量空间映射到低维特征向量空间中去,通过这种方法产生的的特征都不在原始数据中。
4.特征编码
数据集中经常会出现字符串信息,例如男女、高中低等,这类信息不能直接用于算法计算,需要将这些数据转化为数值形式进行编码,便于后期进行建模。
独热编码(one-hot):图中的Elevator和Renovation都是定类型数据。除去缺失值,Elevator分类有电梯和无电梯两种,因此可用01和10表示。Renovation分为有精装,简装,毛坯和其它四种,可用0001/0010/0100/1000表示。

【数据建模】
世界上的可能关系千千万,漫无目标的试探~之间的关系显然是十分低效的。因此假设空间先圈定了一个模型能够表达的关系可能。主要的数据模型有两类:分类问题和回归问题。
分类问题:分类问题是监督学习的一个核心问题,它从数据中学习一个分类决策函数或分类模型,对新的输入进行输出预测,输出变量取有限个离散值。分类在我们日常生活中很常见。
回归问题:回归分析用于预测输入变量(自变量)和输出变量(因变量)之间的关系,特别是当输入变量的值发生变化时,输出变量值随之发生变化。
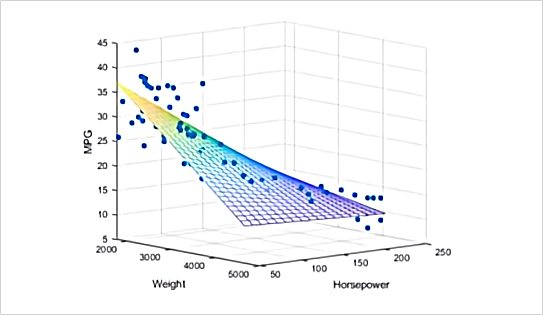
在把一个问题建模的时候一定要考虑好需求,让你的模型更好的与现实问题相对应。
【模型评估】
所谓模型评估,即对模型的泛化能力(性能)进行评估,一方面可以从实验角度进行比较,如交叉验证等;另一方面可以利用具体的性能评价标准,如测试集准确率等。通常来说, 模型的好坏不仅取决于算法和数据,还取决于任务需求。因此,不同的任务往往对应不同的评价指标。
1.性能评价指标-分类
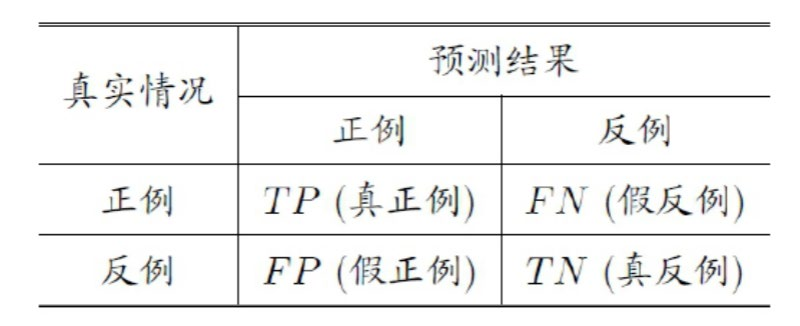
准确率(Accuracy):分类任务中,分类正确(包括正负样本)的记录个数占总记录个数的比。
精确率(Precision):分类正确的正样本个数占分类器所有的正样本个数的比例。
召回率(Recall):也叫查全率,是指在分类中样本中的正例有多少被预测正确了,通常,准确率高时,召回率偏低;召回率高时,准确率偏低。
F1-Score:精确率与召回率的调和平均值,它的值更接近于Precision与Recall中较小的值。
例如,对于地震的预测,我们希望的是召回率非常高,也就是说每次地震我们都希望预测出来;而对于嫌疑人的定罪我们希望是非常准确的,即使有时候放过了一些罪犯(召回率低)。
2.性能评价指标-回归
平均绝对误差(Mean Absolute Error,MAE):平均绝对误差就是指预测值与真实值之间平均相差多大。平均绝对误差能更好地反映预测值误差的实际情况。
均方误差(Mean Squared Error,MSE):观测值与真值偏差的平方和与观测次数的比值。这也是线性回归中最常用的损失函数,线性回归过程中尽量让该损失函数最小。那么模型之间的对比也可以用它来比较。MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。
交叉验证(Cross-Validation):交叉验证,有的时候也称作循环估计(Rotation Estimation),是一种统计学上将数据样本切割成较小子集的实用方法。在给定的建模样本中,拿出大部分样本进行建模型,留小部分样本用刚建立的模型进行预报,并求这小部分样本的预报误差,记录它们的平方加和。这个过程一直进行,直到所有的样本都被预报了一次而且仅被预报一次。把每个样本的预报误差平方加和,称为PRESS(predicted Error Sum of Squares)。
交叉验证的基本思想是把在某种意义下将原始数据(dataset) 进行分组,一部分做为训练集(train set),另一部分做为验证集(validation set)。首先用训练集对分类器进行训练,再利用验证集来测试训练得到的模型(model),以此来做为评价分类器的性能指标。
无论分类还是回归模型,都可以利用交叉验证进行模型评估。
补充:
性能评价指标-分类举例

准确率(Accuracy):分类任务中,分类正确的记录个数占总记录个数的比。
精确率(Precision):分类正确的正样本个数占分类器(预测出来的)所有的正样本个数的比例。—>猜对了多少?
召回率(Recall):也叫查全率,是指在分类中样本正例有多少被预测正确了。—>找出了多少?
F1-Score:精确率与召回率的调和平均值(F1=2·Precision·Recall/(Precision+Recall)),它的值更接近于Precision与Recall中较小的值。
精确率和召回率二者是此消彼长的关系
这句话可以这么理解:我们做核酸检测,希望能够达到比较高的召回率,也就是样本中的正例尽可能预测出来,所以正例会偏多,不想放过可疑的。但是这个时候,会加大预测失误的风险,因此分类正确的指标就会下降。
假设我们手上有60个正样本,40个负样本,我们要找出所有的正样本。系统查找出50个正样本,其中只有40个是真正的正样本,计算上述各指标。
- TP:将正类预测为正类的样本数 40
- FN:将正类预测为负类的样本数 20
- FP:将负类预测为正类的样本数 10
- TN:将负类预测为负类的样本数 30
由此可得:
- 准确率:(40+30)/100 = 70%
- 精确率:40/(40+10) = 80%
- 召回率:40/(40+20) = 67%
①高召回率:假设我们手上有60个正样本,40个负样本,我们要找出所有的正样本。系统查找出55个正样本,其中只有42个是真正的正样本,计算上述各指标。
- TP:将正类预测为正类的样本数 ?
- FN:将正类预测为负类的样本数 ?
- FP:将负类预测为正类的样本数 ?
- TN:将负类预测为负类的样本数 ?
由此可得:
- 准确率:?
- 精确率:?
- 召回率:?
②高精确率:假设我们手上有60个正样本,40个负样本,我们要找出所有的正样本。系统查找出30个正样本,其中只有25个是真正的正样本,计算上述各指标。
- TP:将正类预测为正类的样本数 ?
- FN:将正类预测为负类的样本数 ?
- FP:将负类预测为正类的样本数 ?
- TN:将负类预测为负类的样本数 ?
由此可得:
- 准确率:?
- 精确率:?
- 召回率:?
机器学习的方法论
机器学习的方法论和人类科研的过程有着异曲同工之妙,下面以“机器从牛顿第二定律实验中学习知识”为例,来更加深入理解机器学习(有监督学习)的方法论本质,即在“机器思考”的过程中确定模型的三个关键要素:假设、评价、优化。
案例:机器从牛顿第二定律实验中学习知识
牛顿第二定律是艾萨克·牛顿在1687年于《自然哲学的数学原理》一书中提出的,其常见表述:物体加速度的大小跟作用力成正比,跟物体的质量成反比,与物体质量的倒数成正比。牛顿第二运动定律和第一、第三定律共同组成了牛顿运动定律,阐述了经典力学中基本的运动规律。
在中学课本中,牛顿第二定律有两种实验设计方法:倾斜滑动法和水平拉线法。通过实验,我们可以获取大量数据样本和观测结果。
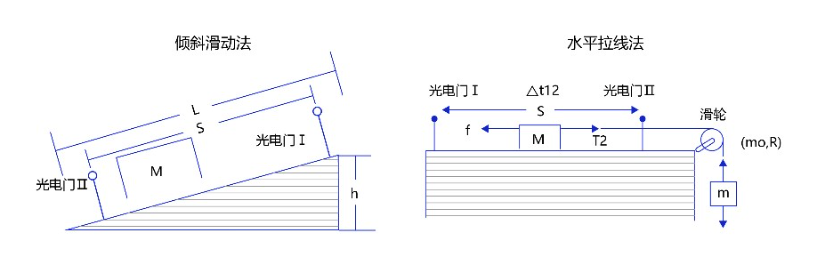
观察实验数据不难猜测,物体的加速度和作用力之间的关系应该是线性关系。因此我们提出假设 ,其中,代表加速度,代表作用力,是待确定的参数。
通过大量实验数据的训练,确定参数是物体质量的倒数,即得到完整的模型公式。
这个有趣的案例演示了机器学习的基本过程,但其中有一个关键点的实现尚不清晰,即:如何确定模型参数?
在牛顿第二定律的案例中,基于对数据的观测,我们提出了线性假设(hypothesis),即作用力和加速度是线性关系,用线性方程表示之后我们使用已有的数据来验证假设的可行性,衡量模型预测值和真实值差距的评价函数也被称为损失函数(loss function)。最小化损失是模型的优化目标,实现损失最小化的方法称为优化算法(optimization),也称为寻解算法(找到使得损失函数最小的参数解),直到模型学习到一个参数$w4,使得损失函数的值最小。
由此可见,模型假设、损失函数和优化算法是构成模型的三个关键要素。
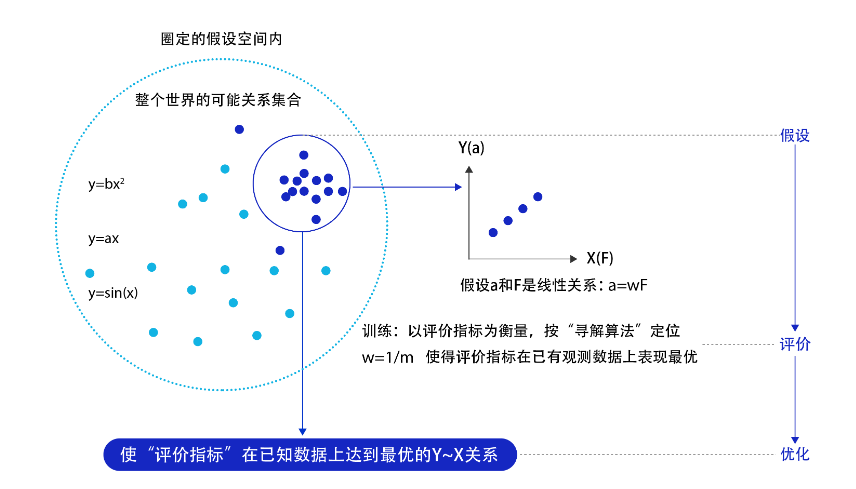
- 模型假设:世界上的可能关系千千万,漫无目标的试探~之间的关系显然是十分低效的。因此假设空间先圈定了一个模型能够表达的关系可能,如蓝色圆圈所示。机器还会进一步在假设圈定的圆圈内寻找最优的~关系,即确定参数。
- 损失函数:寻找最优之前,我们需要先定义什么是最优,即评价一个~关系的好坏的指标。通常衡量该关系是否能很好的拟合现有观测样本,将拟合的误差最小作为优化目标。
- 优化算法:设置了评价指标后,就可以在假设圈定的范围内,将使得评价指标最优(损失函数最小/最拟合已有观测样本)的~关系找出来,这个寻找最优解的方法即为优化算法。最笨的优化算法即按照参数的可能,穷举每一个可能取值来计算损失函数,保留使得损失函数最小的参数作为最终结果。
机器执行学习任务的框架体现了其学习的本质是 “参数估计”(Learning is parameter estimation)。
传统机器学习VS深度学习
相比传统的机器学习算法,深度学习做出了哪些改进呢?其实两者在理论结构上是一致的,即:模型假设、损失函数和优化算法,其根本差别在于假设的复杂度。这种变换已经无法用数学公式表达,因此研究者们借鉴了人脑神经元的结构,设计出基于神经网络的模型。
传统方法:人工特征提取+分类器

- 收集并标注几百张鸢尾花的图片;
- 观察不同的鸢尾花图片,并绞尽脑汁选择或设计一些特征形状,颜色,纹理;
- 根据设计的特征,提取图像的特征,并选择分类器进行训练和测试;
- 结果不好的话,回到第二步。
深度学习方法:提供图像和标签,通过网络自己去学习特征
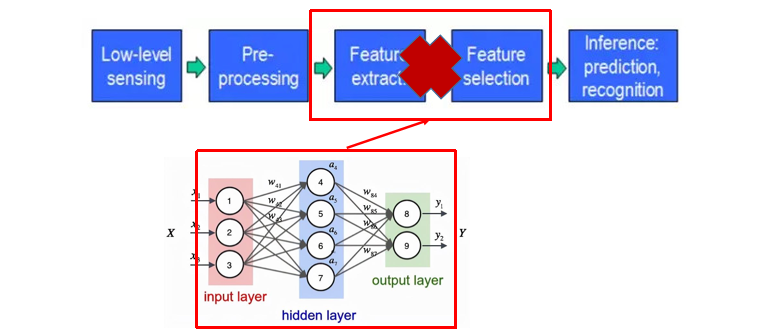
- 收集并标注几千张图像
- 确定网络结构,交给机器绞尽脑汁完成任务
深度学习结构三要素
数字识别是计算机从纸质文档、照片或其他来源接收、理解并识别可读的数字的能力,目前比较受关注的是手写数字识别。手写数字识别是一个典型的图像分类问题,已经被广泛应用于汇款单号识别、手写邮政编码识别等领域,大大缩短了业务处理时间,提升了工作效率和质量。
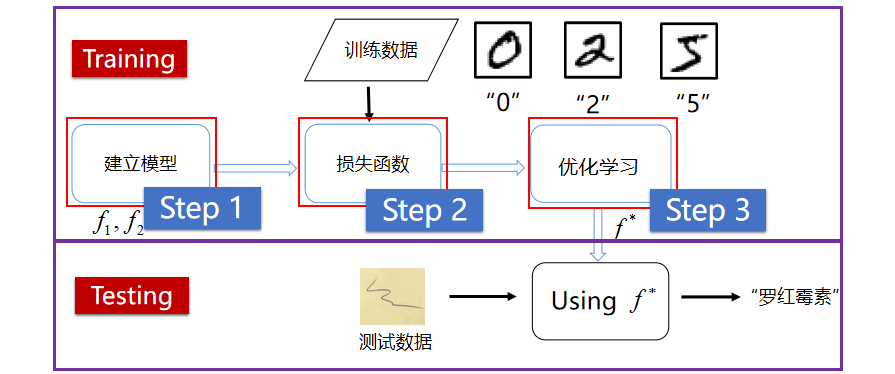
- 建立模型:选择什么样的网络结构/选择多少层数,每层选择多少神经元
- 损失函数:选择常用损失函数,平方误差,交叉熵,…
- 优化学习:梯度下降/反向传播算法
【建立模型】
借鉴了人脑神经元的结构,设计出的神经网络模型可以更好的拟合复杂的数据。
生物神经元
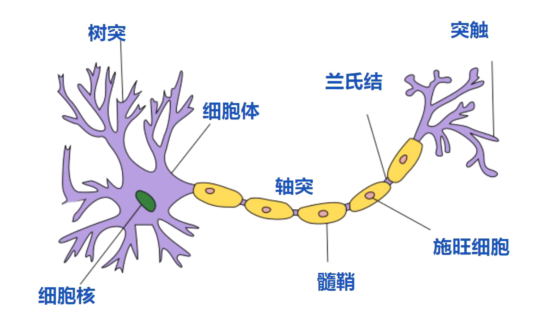
- 每个神经元都是一个多输入单输出的信息处理单元;
- 神经元具有空间整合特性和阈值特性(兴奋和抑制,超过阈值为兴奋,低于是抑制);
- 神经元输入分兴奋性输入和抑制性输入两种类型;
- 神经元输入与输出间有固定的时滞,主要取决于突触延搁(计算耗时)。
M-P神经元
按照生物神经元,我们建立M-P模型。为了使得建模更加简单,以便于进行形式化表达,我们忽略时间整合作用、不应期等复杂因素,并把神经元的突触时延和强度当成常数。
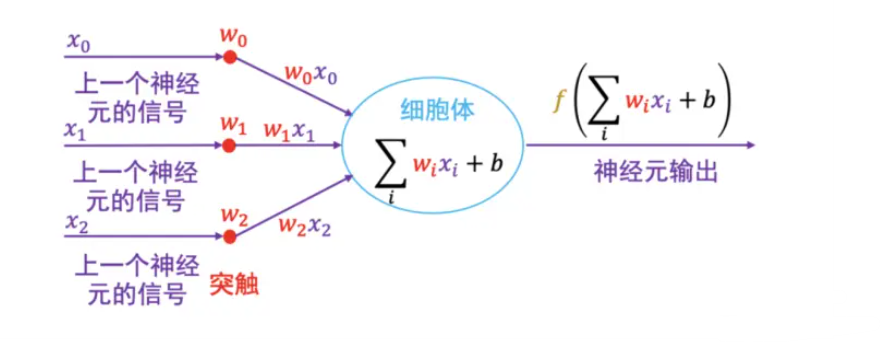
神经网络中每个节点称为神经元,由两部分组成:
- 加权和:将所有输入加权求和。
- 非线性变换(激活函数):加权和的结果经过一个非线性函数变换,让神经元计算具备非线性的能力。
大量这样的节点按照不同的层次排布,形成多层的结构连接起来,即称为神经网络,神经元不同的连接方式构成不同的网络结构。每个神经元都有自己的权重和偏置参数。
【损失函数】
损失函数是模型优化的目标,用于在众多的参数取值中识别最理想的取值,损失函数的计算在训练过程的代码中,每一轮模型训练的过程都相同,分如下三步:
- 先根据输入数据正向计算预测输出;
- 再根据预测值和真实值计算损失;
- 最后根据损失反向传播梯度并更新参数。
【优化学习】
借用古代炼丹的一些名词,我们可以把训练模型中的数据比做炼丹药材,模型比做炼丹炉,火候比做优化器。那么我们知道,同样的药材同样的炼丹炉,但是火候不一样的话,炼出来的丹药千差万别,同样的对于深度学习中训练模型而言,有时候模型性能不好,也许不是数据或者模型本身的原因,而是优化器的原因。
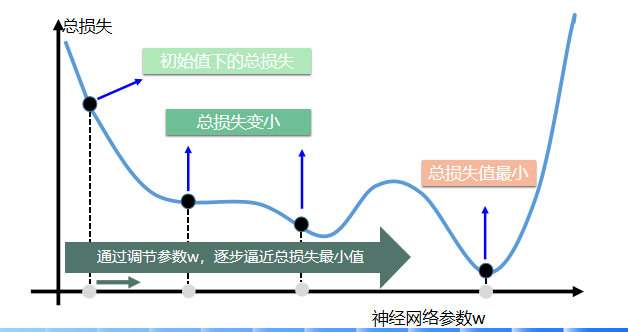
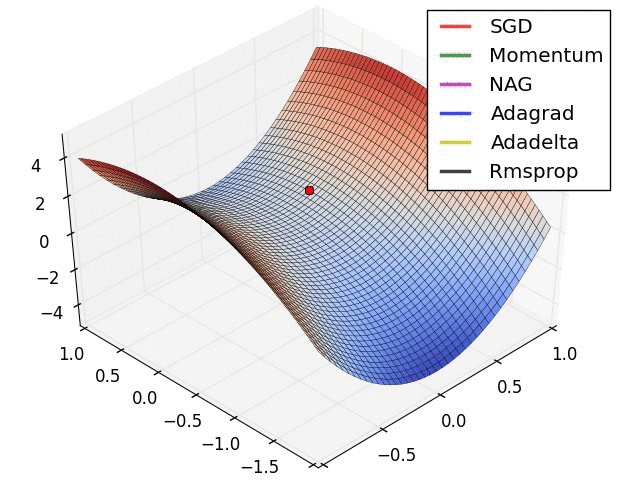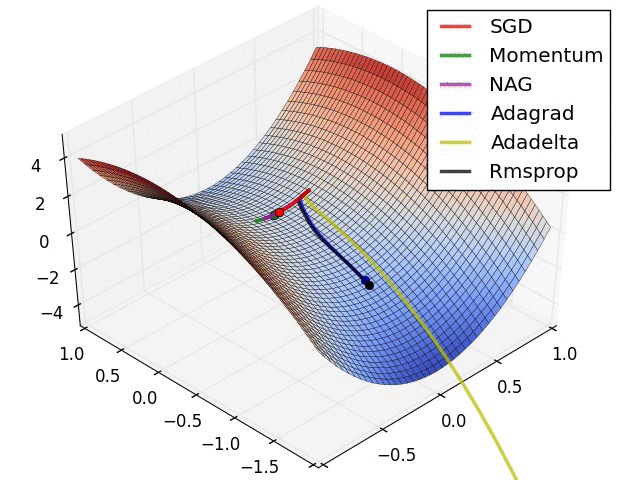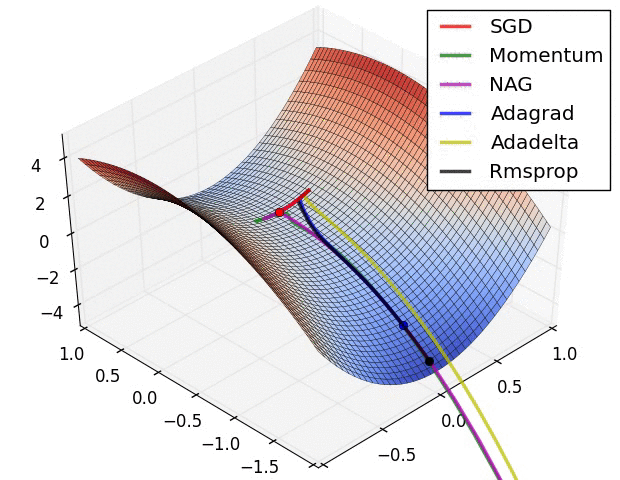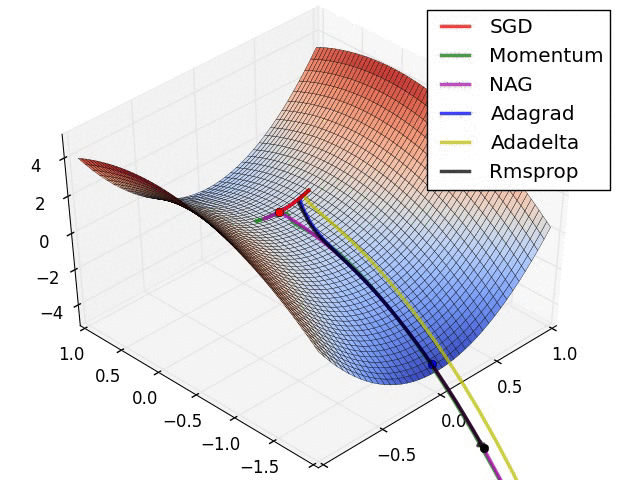
深度学习中的优化问题通常指的是:寻找神经网络上的一组参数,它能显著地降低目标函数。在深度学习中,常见的优化算法包括传统的 SGD,Momentum SGD,AdaGrad,RMSProp 和 Adam 等,我们可以使用一张图来简单看一下这些优化算法各自的性质,后面我们会在优化算法一章中展开讲解。